论书法结构美的数学原理（万字长文，全新视角）

一、一个数字，攻克全部书法结构

书法？和数学有啥关系？莫不是作者要开始生拉硬拽？

非也。

长久以来，学书者普遍持有一种根深蒂固的误解，即认为：学习书法只有临摹这唯一的途径。

邓散木在《怎样临帖》中就说：“（学习书法）除多看多写外，别无捷径可走。”

“书法不可走捷径”，似乎已成定论，笔者听到耳朵都长茧了。

但我研究书法，心心念念一以贯之的目标，就是想找到整个书法的大规律，试图建立一个合乎逻辑的书法理论与创作体系。

民国俞剑华在《书法指南》中说：苟欲求一简单之方法，以统御反复之字体，实为不易。

经过“实为不易”的研究，我是确信已找到这个“简单之方法”的了。算不算捷径暂且不说，足以给诸君提供一条迥异乎过往的思路。是否虚言，请君明辨。

这一切，要从一个数字讲起。

二、过去书法研究方法的局限性

对于书法结构（或称间架、结体、结字）规律的理论研究，始于隋代智果的《心成颂》，至今已1400余年。不客气地说，这些理论不仅没把结字搞清楚，而且越搞越乱。致使大多数人学书法费尽心力，难窥堂奥。

从逻辑学的角度说，古人研究书法最大的局限性，在于他们只懂得使用归纳法，即从经验中总结出规律。

一字有一字之写法，三千字就有三千种写法。那学书法可真是太难了！毕竟汉字何止上万，每个字练个100遍，啥时候是个头。

自然，有些聪明人就着手去总结这三千字的共性出来，这三千字中必然有较类似的某种固定的模式，所谓“规律”是也。市面上最为流行的清人《黄自元结构九十二法》便是此思维的产物。但，即便从3000法减少到92法，结果仍然是不能令人满意的，初学者很少有能把这92法研究透的耐心和意志。到最后，仍然是字帖上有的字经年累月才能学会，字帖上没的字怎么也不会写。那么继续进行归纳，48法、36法又如何呢？

沿着这条线思考下去，你就走进了经验“归纳”的死胡同。

归纳法的先天缺陷，无法保证结论的普遍性和必然性，是无论如何都绕不开的。

不管你如何归纳，以下两个问题是解决不了的。

①普遍性。法则是否绝对完备。108法，讲清楚了书法结构的所有方面吗？万一有些很重要的东西，你的法里没讲到呢？

②必然性。法则是否绝对正确。108法，每一法都绝对正确吗？错一条就是误人子弟啊。

古人的108法、84法、36法，充其量只能算是个人经验的表达，不可称为书法之法。

两千年书法教育陈陈相因，除了“多看多写”、“临摹临摹”便没别的了，其本质原因就在于此。

既然西方哲学给我们带来了“逻辑思维”，带来了“演绎推理”，这个冗长的循环也该就此跳出了。

所谓演绎法，就是先确定一个具有普遍性和必然性的绝对真理，以此真理为出发点、大原则，进行形式逻辑的推演。只要大原则正确，推理结果就正确。所谓：万变不离其宗。

假设古往今来，所有好看的字，都受某个终极规律的支配。若掌握了这个“终极规律”，我们岂不是一下子就突破了所有的字。

这个规律存在吗？

好看的本质到底是什么？

譬如下面一个“務”字，好看在哪里？怎么解释？

本文将从逻辑上去推理汉字何以好看，为读者解释清楚：当我们说某个字好看时，我们到底是在指什么？若读者能跟紧我的思路，时机一到，定会恍然大悟，如金鳞透网，顿觉天地宽阔。

那时你就会觉得，书法和数学，真是大有关系嘞。

三、对美的认知存在大众普遍的共识

在《服饰色彩搭配》这本书中，有一段话，对我探求书法规律有着决定性的启发意义。

作者说在服装设计中：

“各部件是形式的客观要素，它们的组合则是按照一定的形式法则设计的。或对称、或均衡、或具有一定的比例关系。这些形式塑造出服饰的整体情调。单从形式条件来评价服饰作品时，对于美或丑的感觉在大多数人中存在着一种基本相通的共识——这就是形式美的法则。”

我们经常说“萝卜青菜，各有所爱”，说艺术无定法。但如果大多数人都承认某物是美的（如王羲之书法），那就说明对于美的认知，存在着大众普遍的共识。

这个大众普遍的共识，就是我所说的演绎法的出发点（这里先忽略掉小部分人的特殊审美趣味）。

也就是说，我研究书法，并不是从一个个好看的字开始，溯源而上，去寻求它们的共同规律。而是从“美的大原则”开始，顺流而下，推演出一套东西。如果“美的大原则”正确，那我的这套东西就正确，正因为那些好看的字符合了我的这套东西，它们才好看。

这是我的基本思路。

“过程哲学”创始人怀特海在《思维的方式》中说：所有体系化的思想，都必须始于前提。

我体系的前提就是“美的大原则”，就是“大众普遍的共识”。

既然是共识，那就你知我知，毫无神秘性。

没错，你应该猜到，这个能攻克所有汉字结构的数字，就是黄金分割率。

我的体系由此发端。

四、产生美感的三个“公理”

你看着这张图，汉字结构好看的奥秘，全在这里面。

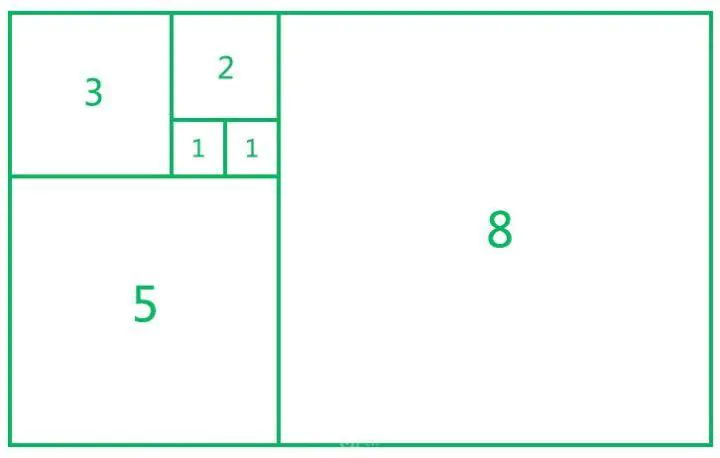
如果能理解，就不必往下看了。不能理解，且听我道来。

公理①：对称能带来美感。

此理人所共知，不再赘言。

它在比例上表示为1:1。

譬如写个“十”字，横写完后，竖写在哪才好看呢，很明显，可以写在横的中点。

公理②：黄金分割能带来美感。

这里我们默认黄金分割能带来美感，把它作为无需证明的“公理”来使用。至于黄金分割为什么能带来美感，本文从略，后续会写一篇文章《黄金分割带来美感的深层次原因》进行探讨。

何为黄金分割？

一点把线段分成两段，短线段与长线段的比值等于长线段与全长的比值，则此点为线段的黄金分割点。

此比值可用数学方法求出，即大名鼎鼎的0.618。

我们用此理论来写个“十”字，一横一竖两条线。

当我们写完横之后，横的长度确定了，竖放在哪里呢？虽然有无数个点可放，但现在根据公理，竖放在黄金分割点上是最好看的。（这里有个问题，线段上有两个黄金分割点，放在右点比左点更好看，此问题涉及到心理学，本文暂不论述。）

虽然对称能带来美感，黄金分割也能带来美感，但好像竖放在黄金分割点上比在对称点上的美感更高级一点似的。完全对称略显呆板。

请注意，我们这个“十”字仍未写完。

横和竖的相对位置虽然确定下来了，但是横和竖的长度该如何规定才有美感呢？

如果我的横很短很短，竖很长很长，毫无疑问这个字即使符合上述的黄金分割，也是不具美感的。如下图。

假设横的长度为单位1，显然竖的长度不能是100、10000，竖的长度一定会在某个范围内波动，才具有美感，超出这个范围，我们的眼睛便会判断它是丑的。这个范围应该怎么确定呢？

如果我们把“十”的横竖连起来，做出一个外框矩形。那么，这个矩形太扁了不好看，太窄了也不好看（太扁和太窄实际上是一回事，只是同一个矩形横放竖放而已）。

那矩形的长宽比在什么范围内才算好看呢？

公理，公理！我们再次回到黄金分割。

想必你听说过“黄金矩形”这个概念。

我们说矩形的两个边之比为黄金分割比例（黄金矩形）的话，是临界的美感。

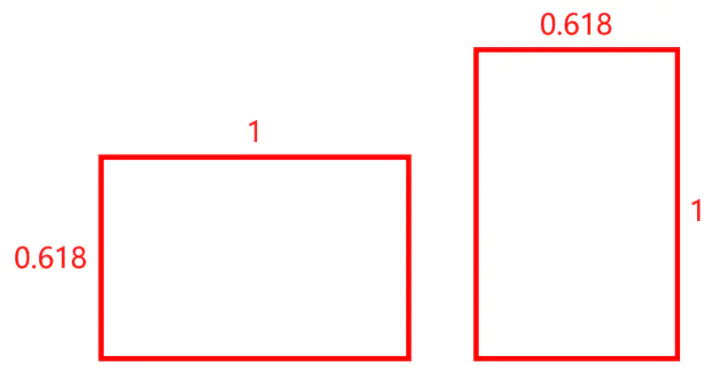
即“美的矩形”的长宽比应为0.618:1~1:0.618，即0.618~1.618。

至于小于0.618的或大于1.618的矩形，我们暂时就认为其比例不协调，并定义其为“丑”。

据说，蒙娜丽莎脸的比例，就完美符合黄金矩形。

既然黄金矩形使蒙娜丽莎的脸型协调好看，难道不能使汉字的外形协调好看吗？

不过从视觉上，0.618这个比例是小数，无法一眼找到，不利于书法操作。

于是我们不妨寻求其在整数比上的近似。

2/3 = 0.667 ≈ 0.618。

我们用整数比2:3去近似黄金分割比例，则公理②可以写成。

公理②：黄金分割能带来美感，比例为2:3。

再看最后一条。

公理③：三等分能带来美感，比例为1:1:1。

这一条其实可以由前两条公理推导出来。

若把对称理解为二等分（1:1），则三等分（1:1:1）可作为特殊形式的对称。

用黄金分割来解释的话，则短边为1，长边为2，全长为3。

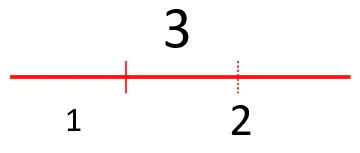
根据黄金分割的定义，1:2（短线段比长线段）就约等于2:3（长线段比总长）。

也就是说1:2也是黄金分割在整数比上的近似，只不过精度没有2:3高。

至此，整理下产生美感的三个“公理”，或者说三种比例。

对称，比例为1:1。

三等分，比例为1:1:1。

黄金分割，比例为2:3。

马上来进行运用。

五、所有好看的字共同遵守的法则

只要我们将这三个比例付诸书法实践，神奇的事情瞬间就会发生。

“相”字怎么写？

首先，外接矩形的长宽比要顺眼（具体多少是顺眼，根据个人审美的不同，可以在在0.618~1.618之间波动）；其次，左边“木”和右边“目”，比例1:1（对称）。

看见没，你这么写，这个字就是好看的（暂且忽略掉些许误差，以后会完善）。

这背后的逻辑是，实际存在一个顺眼的矩形形状，沿着顺眼比例的中线切分，我们认为这个图形是好看的。这个矩形，及矩形的切割方法，符合某种秩序（对称、三等分、黄金分割），我们人类的眼睛本能地感觉到了这个秩序，于是便感觉它好看、顺眼。

这时，把“相”字放到这个框里，这个“相”便继承了矩形及矩形分割的好看性，于是我们认为这个字也是好看的。

因为这个字背后遵循着一个秩序！

亚里士多德说：“美的主要形式是秩序、匀称、明确”，“一个美的事物……不但它的各部分应有一定的安排，而且它的体积也应有一定的大小，因为美要靠体积与安排。”

普通人通过感性可以本能地察觉到这个秩序（因为存在大众普遍的共识），察觉到“体积与安排”，发出一声“这个字挺好看的”感慨，但是因为缺乏研究，他却不知道好看在哪里。

唐代书论家张怀瓘云：视之不见，考之则彰。

说得多么明白！我们有理由相信古人是懂这些道理的，不然说不出这么精准、严丝合缝的话。

继续推演，左右结构的字，“物”、“理”等等，本质上和“相”都是一样的，从数学角度上看，没有任何区别。

那“谢”呢？三等分嘛。容易。

那上下呢？“盖”、“雲”？还不是一回事，上下二等分罢了。

包世臣的《艺舟双楫》中记载了清人黄小仲的一句话：“书之道，妙在左右有牝牡相得之致。”左右相得，上下不也要相得吗？

何谓“相得”？何谓“适宜”？何谓“协调”？何谓“法度”？

大众普遍的共识。

黄金分割是也！

那再复杂一点的字？比如“繁”。

依然是如此，只不过多切割几次而已。

我们构建一个稍瘦的比较顺眼的矩形。将其横向二等分，就是上下“敏”和“系”的比例。上面的“敏”呢，再来个竖向二等分。下面的“系”，上下继续二等分。

妙就妙在，我们可以无限分下去。“敏”的“每”，上面“人”和下面“母”，上1下2，“母”的横再等分。

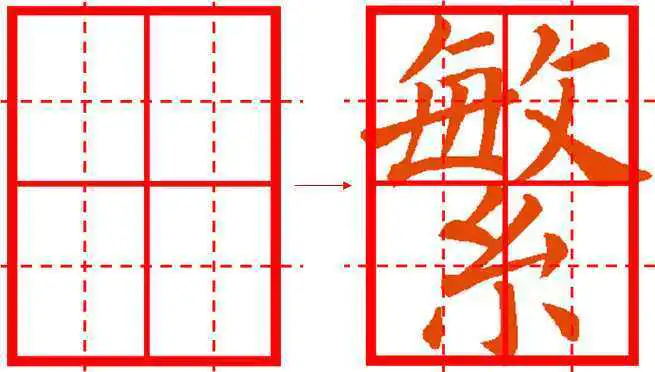
这其中的逻辑是，我们不断用符合黄金分割美感的分割方法去分割一个本来就很顺眼的矩形，然后把“繁”字放到其中，这个“繁”字就继承了该矩形及矩形分割方法的秩序。当普通人看到它时，本能地感受到了秩序，就莫名其妙地认为这个“繁”字是好看的。

书法结构好看之本质，就在于此！

对于每个字，自己分割分割，设计一下比例和形状，在心里推演一下，即使不参考字帖，也能知道个大概。读帖时，也可用此方法去分析古人的字，从逻辑上，所有好看的字必然符合此法。（当然，不可能也没必要完全做到数学上精准的1:1，1:2，允许有一定的误差。）

善书者眼中皆是比例、形状、关系，忘却字形为何物，所谓“目无全牛”是也。

想想“庖丁解牛”的典故，庖丁眼中的牛绝不是普通人眼中的“全牛”，而是各种骨隙如同X光照射般暴露在眼前。是一个又一个“下刀处”。

我们写字时必当同此感觉乃可。字形要退居幕后，眼中看到的是一组又一组点线面的关系，心中不断推演着各种比例和形状。如孙过庭的精辟之语，“亦犹弘羊之心，预乎无际；庖丁之目，不见全牛”。

董其昌说：书家之结字，画家之皴法，一了百了，一差百差。

你怎么能一了百了，突然之间一下子把所有的字都掌握呢？

若不去揭示现象背后的本质（这里很像哲学中所谓“共相”），是不可能做到的。

临摹临摹，无视法理的存在，而去死写形迹，不敢说白费功夫，起码是效率低下。如同巴甫洛夫之狗，条件反射而已。

明白了三种美的比例，所有的字在你眼前瞬间褪去神秘的面纱，随便一想就知道咋写了。当然，我绝没有否定临摹字帖的价值，很多细微处、精妙处，不看字帖，自己是鼓捣不出来的。但是，整个字的大体脉络，大框架，掌握了，写出来的字也就丑不到哪去。

试一下。比如“眼前”，“眼”，左1右1，右边上1下1（或上2下3）。“前”，上1下2，下面左1右1（或左3右2）。

非常简单。不过是来来回回倒腾那些比例而已。

这种比例方法虽然好用，却会产生两个问题或者说两个不足。

①这样写太死板了。

②字帖上有的字有些部分超出了你的比例线，怎么解释？

如下面的“儀”字，主体部分虽然大致符合比例，但右下角的斜钩出去了，这不是说明你的比例是胡扯的吗？

别急，我后面有简单的方法处理这两个问题，使其更完善，请暂时先包容下这些小瑕疵。

米芾说过：真字甚易，唯体势难。

以前看到这话，你根本无法理解。真书，即楷书，这么难，难死了，好几年也写不好，怎么可能“甚易”呢？

现在呢？

知道所有的字都守着同一个规律，作何感想？

米芾早已看穿一切。

我们写字的本质也就变成了，不断去制造具有美感潜质的比例和形状。

达芬奇说：美感完全建立在各部分之间神圣的比例关系上。

香奈儿创始人可可·香奈儿说：时尚就像建筑，一切关乎比例。

一切关乎比例，此语道破天机。

六、栅格系统

使用比例系统辅助制造美感，在书法中看似创新，在西方艺术（如设计、摄影、构图）中，却是早已有之。

栅格系统英文为“grid systems”，也有人翻译为“网格系统”，指利用一系列垂直和水平的参考线，将页面分割成若干个有规律的列或格子，再以这些格子为基准，控制页面元素之间的对齐和比例关系，从而搭建出一个具有高度秩序性的页面框架。

例如谷歌的Material Design中，将整个页面看做是一个网格，所有页面元素都与网格线对齐，并且将这一规则贯穿于整个产品的设计中。

掌握栅格系统是从事版式设计所必须具备的基础修养之一，栅格系统作为一种行之有效的版式设计法则，它使所有的版面构成元素之间的协调一致称为可能。

因为书法结字相对比较简单，只用到三个比例即可，栅格系统则需要更丰富的比例，但原理无二。

版式设计中的栅格系统

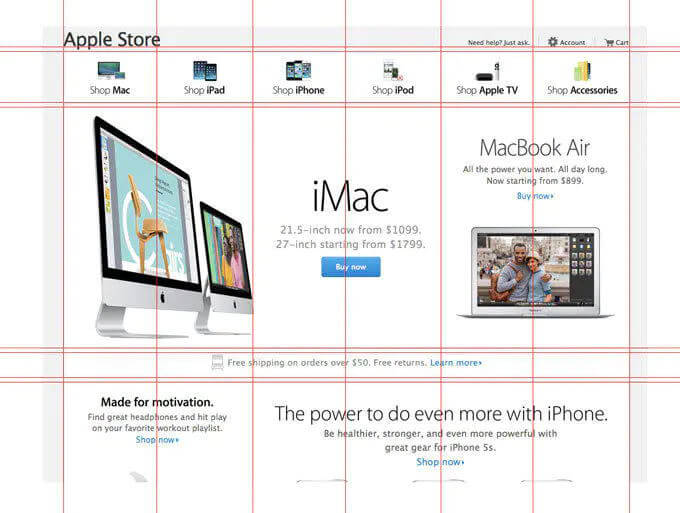
网页设计中的栅格系统

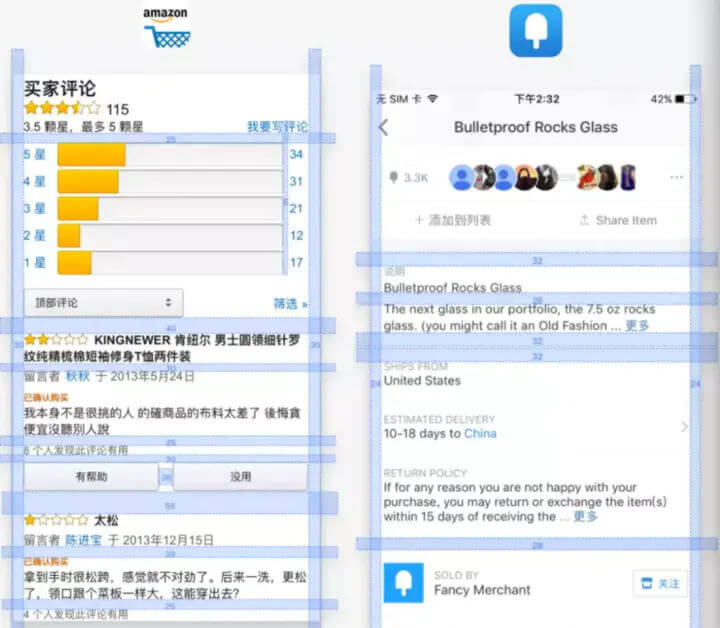
UI设计中的栅格系统

七、九宫格

“栅格系统”始于西方，盛于当代。然而在中国，却也称得上“古已有之”。

古人早已在练字中熟练使用简化版的“栅格系统”了，这就是著名的九宫格。

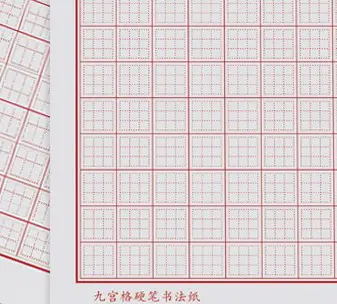
据传，九宫格是唐代欧阳询发明的。唐代是楷书的鼎盛时期，注重法度，欧体又被誉为“楷书极则”。所传应非空穴来风。

九宫格到底有什么用呢?

清人刘熙载在《艺概》中也说：欲明书势，须识九宫。

平时大家也都听说过九宫格，甚至使用过，你的使用方法正确吗？如果你像下图这样使用，那就大错特错了，完全没get到九宫格的点。

九宫格即是用三等分近似黄金分割的简易栅格系统。

左右结构、上下结构的字，1：2，2：1，基本分割方法都在其中，中间的四个焦点即是4个黄金分割点。而1：1很好识别，无需辅助线。

就是说，用九宫格可以表示出绝大多数字的结体。

你仔细看着它。

看到了没？

里面有“花”，有“露”，有“徒”，有“物”。

从小到大，你学过的每一篇课文，接触到的每一个字，都在这里面。

所有中国人用汉字写出的东西，都在这里面。

这就是汉字的万能公式！

弄懂它，就破解了汉字好看的奥秘。

如下图这样，整个字写在了中宫附近，四周留出这么多空白，其他八宫还有什么作用呢？

很显然，书者未能理解九宫格的真意。

不止今人，古人也未必都明白九宫格的奥妙所在。

清代王澍《翰墨指南》云：“结构之法须用唐人九宫式，则间架密致，有斗笋接缝之妙矣。九宫者，每一格中有九小格如井字样，临帖时牢记某点在某格之中，某画在某格之内。记熟则出笔自肖法帖，且能伸能缩，惟我所欲矣。”

元代陈绎曾《翰林要诀》云：九宫结构，随字点画多少疏密，各有停分，作九九八十一分，界画分布，以便临摹。

以上二位前辈只把九宫格当成临摹的“坐标定位”，最终目的是“记熟”。把九宫格用成了死记硬背的工具，大材小用。

也有些古人真的在用比例意识分析汉字结构。

元人所作《书法三昧》中有言：布置如“中” 字孤单则居中。“龙” 字相并则分左右为二停。“冲” 字则分为三停。“云” 字则分为上下二停。凡四方八面，点画皆拱中心。

除了没有发现2:3，二等分和三等分他们都注意到了。

可惜古人不能把比例系统理论化，仅停留在个人经验的表达，为大众所忽视。

《书法三昧》这本书赵孟頫曾传抄过，想必松雪作字时，应有一“比例系统”成竹于胸焉。

八、三比例之统一

如下三个带来美感的比例：

①对称 1:1；

②三等分 1:1:1；

③黄金分割 2:3。

即是我所说的演绎推理的前提，是“美的大原则”。

然而一个问题使我心有不安：为什么是三个？

美的大原则，不应该是只有一个至高原则吗？三个算是怎么回事？

因而三个比例需要进行统一。

对称，即二等分，和三等分一起，可以统一到“等分”上。

如果黄金分割也可看成“等分”的话，那三比例就成一个了。

貌似可以。当我们用2:3去近似黄金分割时，黄金分割不就是五等分吗？

按这个思路，我们的比例可以写成：

二等分，1:1；

三等分，1:1:1；

四等分，1:1:1:1；

五等分，（1:1）:（1:1:1）。

因为四等分即两次二等分，所以可删去。

那带来美感的三个比例，其本质即 “等分”。

等分能带来美感！

为求方便，我用一个字来代表“等分”。

那就是“均”。

明代项穆在《书法雅言》中总结了书法最重要的原则，他说：大率书有三戒，初书分布戒不均与欹，继知规矩戒不活与滞，终能纯熟戒狂怪与俗。

“戒不均”就是要追求“均”，我的理论和古人的感悟是严丝合缝的。

民国张树候《书法真诠》云：吾谓作字之道，其结体不过一“称”字；布白不过一“匀”字。

“匀称”，看似二字，其实也不过就是一个“均”。

外行写字，字形是散乱的、任意的、杂多的，而内行会做到“均”，把杂多的笔画整理出一种秩序，这便是书法入门与否的标志。

“对规律性、秩序感的形式追求是人类设计的永远审美理想。”（黄柏青《设计美学导论》）

九、斐波那契数列

我对三比例的统一，是生猛粗暴的，有点强行往“等分”，往“均”上靠拢的意思。

实际上，它们有更科学的统一方法，这就是数学上著名的“斐波那契数列”。

1、1、2、3、5、8、13、21、34、55、89、144、233……

观察可以发现，后一个数字，是前两个数字之和。并且如果把前后两个数字相除，获得的数值就会越来越趋近一个数字，1/2=0.5，2/3≈0.67，3/5=0.6，5/8=0.625，8/13≈0.615，… ，144/233≈0.618。

当数列的最后两项趋近于无穷大的时候，前后两个数字之比即完全等于黄金分割的数值。

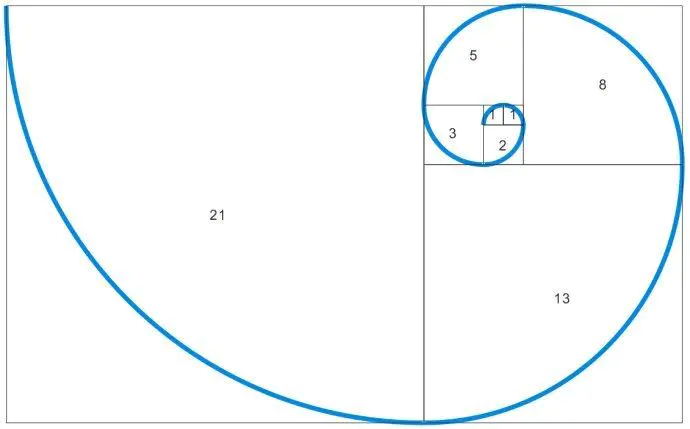
我们重点看这个数列的前4项：

1、1、2、3、5、8、13、21、34、55、89、144、233……

1:1，即二等分，即对称。

1:2，即1:1:1，即三等分。

2:3，即五等分，即黄金分割。

即是说，依照数学原理，二等分和三等分是一种特殊的、近似的、简易的黄金分割。

在数学上，三比例可以统一为黄金分割！

至此，我所谓的“美的大原则”，“大众普遍的共识”，便只有一个黄金分割，没别的！

我之所以多此一举地把三比例统一为“等分”，一是为了叙述简洁，只用一个“均”字便可代表；二是为了和古人的经验保持一致，古人没有“黄金分割”一说，但很多人都提到过结构要做到“均”。

如包世臣在《艺舟双楫》中说：“字有九宫。九宫者，每字为方格，外界极肥，格内用细画界一“井”字，以均布其点画也。”

均布其点画，说得多明白！

包世臣看出了九宫格的真理。

十、模度

在二维的平面设计中使用比例，有一套栅格系统。

在三维的建筑设计中，同样有人注意到了比例的强大，并发明了一套系统。

那就是法国著名建筑师勒·柯布西耶和他的模度。

柯布西耶认为一个身高6英尺（183cm）的男子，其身体比例是具有美感的，作为他推理的出发点。

既然6英尺的男子具有美感，那么研究其身上比例，并把这些比例挪用到建筑上，建筑就自然而然“继承”了美感。

都有哪些比例呢？

达芬奇曾发现：人的身高与脐高符合黄金比。

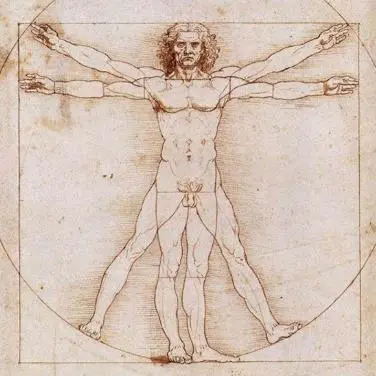
柯布西耶发现：人的举手高是脐高的二倍。

举起手的人给出了比例的关键点：足、肚脐、头、举起手的指尖。

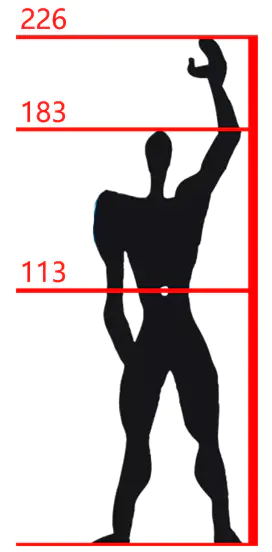
经过测量，身高183cm的人，脐高为113cm，举手高为226cm。

113/183 ≈ 0.617；

226/113 ≈ 2。

所以肚脐是身高的黄金分割点，是举手高的中点。

而指尖到头和头到肚脐的比例同样是黄金比：

（226-183）/（183-113） ≈ 0.614。

那么从指尖到脚的各段长度，就是一段斐波那契数列（如同1,2,3）。

它包含了数学上最简单也是最有力的变化，即单位、倍数、黄金比。

柯布西耶以人的脐高为标准，按黄金比拓展了一系列的尺寸，称为红尺；以人的举手高为标准，按黄金比拓展了一系列的尺寸，称为蓝尺。

建筑设计时，需要尺寸，就直接从红尺或蓝尺（或二者相减）中去找，既省事方便，又保证了每个尺寸都在一个更大的秩序中有其位置。

如大门高度选一个尺寸，房屋高度选一个尺寸，这两个尺寸其实是有黄金比暗含其中的。

多么巧妙的智慧！

“模度是吾师穷其一生，努力探索如何使房子称为“建筑”而创造出的一个工具。……其目的是为建筑以及工业设计提供一个符合人体尺度的、具有和谐比例关系的尺寸控制工具。”（吉坂隆《模度》日文版序言）

爱因斯坦曾与柯布西耶有过对谈，他评价说：此比例系统极易产生美妙形式，很难产生丑陋形式。

那么，当我们把这个比例系统（1,1,2,3）运用到书法上时，也应是极易产生美妙形式，很难产生丑陋形式的。

在这个比例系统中，我们的书法异常简洁，只用了3个“尺寸”（1,2,3），那建筑中需要多少个呢？

马赛公寓的设计，从整体布局到细部的各个尺寸都在模度的控制之中。

柯布西耶让事务所成员作出了所有尺寸的目录。

发现只需要15个基本尺寸——

“15！”

柯布西耶说：

让我们欢呼数的伟大吧！

十一、极坐标：完美的数形结合

如前所言， “法”要具备普遍性和必然性。

我们把黄金分割当成公理来使用，必然性是保证了，那普遍性呢？

一个“均”字，是完备的吗？能解释书法结构的方方面面吗？

显然不能！

那欠缺在何处呢？

我从高中起，一直有个执念，就想把一个字往坐标系里放，然后试图用数学思维研究书法结构。但我一直没鼓捣出来，因为我放的是普通的坐标系。

有次，我灵机一动，往极坐标系里放放会怎样呢？

我们知道，在极坐标中，对于平面内任意一点，都可用相对于原点的一个长度和一个角度来表示。

关键就在这里，长度和角度！

平面内的任何图形，在极坐标中都可以用长度和角度表示出来。换言之，长度和角度是完备的。

书法结构作为平面内的一种图形，无外乎长度和角度！

如果我研究透了长度和角度，就研究透了书法结构。

很显然，并不是所有的长度都具有美感，所有的角度都具有美感。

那么我们必然要对长度和角度进行优选。

把长度进行优选，其结果——

  就是“均”！

把角度进行优选呢？

依照比例系统，180°进行等分，就是90°，也就是书法中的“横平竖直”（也即栅格系统中的横竖辅助线）。我把它同样用一个字来表示，就是“正”！项穆的那句话“初学分布，戒不均与欹”，“欹”就是斜，“戒欹”就是不要斜，就是正。

长度 → 均。

角度 → 正。

因为在坐标平面中长度和角度是完备的，所以在书法结构中我的“正”和“均”也是完备的。

证毕。

结论：

黄金分割（比例系统）保证了必然性。

正和均（极坐标系）保证了普遍性。

十二、秩序与反秩序

然而，练过字的都知道：并没有真正的横平竖直！

高手写字，横和竖都是有倾斜的。这如何解释？

我们要把“正”和“均”再做一次统一。

为什么正均能带来美感呢？为什么栅格系统能带来美感呢？为什么整齐、等分能带来美感呢？

这个问题，我在后续文章《论书法结构美的心理学原理》中会进行详细探讨，在此只说个简易版本。

这是因为正和均的本质，即是秩序。

美学大家贡布里希曾说“有一种秩序感的存在，它表现在所有的设计风格中，而且，我相信它的根在人类的生物遗传之中。”（《秩序感——装饰艺术的心理学研究》）

柯布西耶在《模度》中说：

“秩序是真正的生命之匙。对秩序的探寻，使得人类与其他物种区别开来。通过秩序来统治混乱的欲望反映了人类的深层次精神追求。”

对秩序的追求是人的本能。（有心理学实验支持，以后再讲。）

20世纪美国心理学家马斯洛“需求层次理论”指出： 我们每一个人对安全、稳定、秩序的需求，是仅次于生理需求的最为基本的需求。

所以秩序能带来美感，整齐的排版能带来美感，均匀的布局能带来美感。

复杂就复杂在，人不止要满足本能，更要超越本能。

“仓廪实而知礼节，衣食足而知荣辱”。

秩序并不是艺术的终极，艺术还要反秩序。

马斯洛需求层次理论：生理需求、安全需求、社交需求、尊重需求、自我实现需求。

对秩序的需求，在安全需求层面，只是人的底层需求。

人的最高需求是自我实现！

若书法只有正均，是做不到自我实现的。

所以我们需要在保证大秩序的同时，进行一定的反秩序。

所以没有真正的横平竖直。

用现代的语言说，叫秩序和反秩序。用古人的话，就是“阴阳”。

什么是艺术？

刘熙载在《艺概》中，开篇第一句话就是：艺者，道之形也。

艺术，是道的外在显现。

何为道？《易经》中说：一阴一阳之谓道。道的本质即是阴与阳的关系。

我们看黄金分割这种东西，实际上与太极图异曲同工。太极图要表现的，阴中有阳、阳中有阴，不就是阴阳量的配比吗？阴、阳，并不是均等静止的，而是动态变化，相互转换的。

黄金分割不正是阴阳配比中一个比较舒服的点吗？

比起对称，黄金分割更有动感，存在更多变化的可能。

黄金分割便是道在比例上的一个体现！

再用西方的话进行描述：黄金分割是几千年来人们基于对自然世界的观察，以几何和比例的方式总结的美学规律，柯布西耶称它为 “确定任何事物的标尺”，是通过“秩序”与宇宙力相接触的点，“秩序”通过几何和比例的方式表达，而成为神圣的原理。（高宏宇《神圣的比例——勒·柯布西耶的“模度”》）

想通这一点，那么黄金分割就属于“道”，属于“宇宙力”的范围了，是自然界的某种超然的法则，万物默默遵循其运行而不自知。

而我们力求把书法写好看的过程，我们执笔书写下的每一条线，都是对这个自然界神理、对道的模拟与复现。

从此刻起，如果你从一篇小小的书法作品中体悟出宇宙人生，应无须感到任何惊讶了。

（在后续文章《论书法结构美的哲学原理》中会对“秩序和反秩序”进行哲学和美学层面的详细解释。）

话说回来，如果我的正均不是完备的，正均之外，还要再加点什么呢？

一个字——“变”！

十三、正均变

正、均、变，才是终极之法。

还记得“儀”字的斜钩出格了吗？那便是“变”在起作用。

先用“正均”定一个大框架、大秩序，再用“变”去反掉这个秩序。

我把变掉“正”，称为“破正”；变掉“均”，称为“破均”。

混乱的字结构 → 正、均 → 破正、破均 → 好看的字结构。

这便是我的“正均变”书法体系。

如何“破正”、“破均”，会有文章详谈。

仍需注意：我所倡导的法，倡导的三种比例，不是限制，而是解放。

就如同科学规律不是约束而是生产力一样。

因为“变”的存在，我并不会把你限制在一个封闭的正均体系之中。

哲学家怀特海说：我们要有体系，但体系应该是开放的。换言之，我们应当保持对体系局限性的敏感度。在现有体系之外总会有模糊之处，留待细节的深入。

本文只是开头。

用此体系去解释传统的书法经验，如中宫收紧、主笔、重心、宁左勿右、宁上勿下等，披荆斩棘，摧枯拉朽，百试不爽。不仅易于理解，而且易于操作。

我会用一系列文章进行推演，保证合乎逻辑，助你逐渐使用理性分析而非个人经验审视书法。

这是一条前所未有的通途。

你瞧！

那乱麻一样纷繁复杂的书法结构，成千上万的汉字字形，古今所有书家穷极努力、穷极想象所能达到的境界，诸家、诸体、诸字……

无非，正、均、变，而已。

回答开头的问题，“務”字好看在哪？

画一下就知道咯。

附录、启功先生的“黄金结字律”

启功先生有诗云：

用笔何如结字难，纵横聚散最相关。

一从证得黄金律，顿觉全牛骨隙宽。

（《论书绝句一百首》第99首）

“黄金结字律”是启功在长期观察、临摹和测量北朝和唐人名碑的过程中发现的一套楷书结字规律。

注意，启功的“黄金律”是根据字帖归纳得来的，是经验的总结。只不过古人停留在108法、36法，而启功归纳到了1法（黄金分割）的级别，可谓创举。

把他的黄金律放在文末，是为了给我的体系提供一个力证。

因为我的体系是自上而下演绎推理得来，说得再天花乱坠，用到字上不符合也没用。启功的经验总结，正好补全了空洞的理论，说明字是符合黄金律，符合推理结果的，这样真理才能“比翼双飞”。

启功先生认为一个字的重心并不是一点而是四点，他曾说，“其法将每大方格纵横各划十三小方格，中间三小格纵横成十字路，每行小格为五三五。自左上一交叉点言，其上左俱为五，其下其右俱为八。此十字路中四交叉点，各为五比八之位置，合乎黄金分割之理焉。”

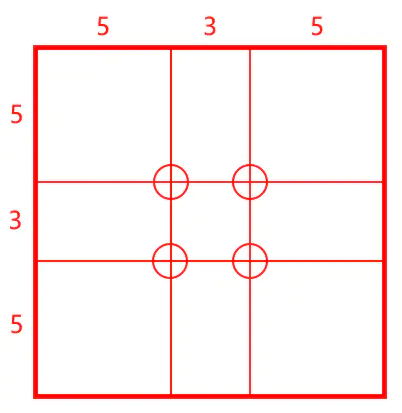
当一个字的主要笔画都经过这四个点（在国外的摄影理论里把这4个点称为“趣味中心”）时，这个字写出来就中宫收紧、外势伸展，因而字形妍美漂亮。

我们发现，启功的“黄金律”其实就是更精确化的“九宫格”。

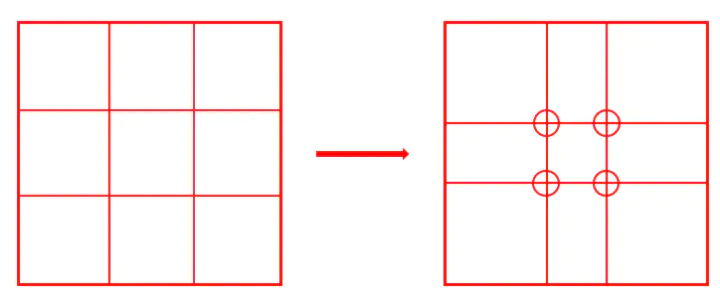
九宫格用1:2、2:3近似黄金律；启功用3:5、5:8近似黄金律。

总之都逃不过斐波那契数列（1,1,2,3,5,8,13……）。

我的体系，不在于创造某种习字格，或让大家理解习字格。

而是要让大家懂得格子（栅格系统、模度）背后的道理，并以此为演绎推理的出发点，推出更多更普适的东西。

敬请期待。

作者：亦斯书法
链接：https://www.jianshu.com/p/c1c3e9643b1a
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。